中国网/中国发展门户网讯 人类进入大科学时代后,“模拟”作为“理论”“实验”以外重要的补充技术手段,成为科学研究的第3个支柱。从表现形式看,科学研究可以被视为建立模型(modeling)的过程。而模拟(simulation)则是所建立的科学模型在计算机上的运行过程。最早期的计算机模拟(computer simulation)可以追溯到第二次世界大战之后,是专门针对核物理学和气象学研究的一种开创性的科学工具。后来,在越来越多的学科中,计算机模拟变得愈发重要,并不断衍生出计算和其他领域交叉的学科,如:计算物理、计算化学和计算生物学等学科。Weaver在1948年撰文指出:人类解决有序复杂问题并实现科学新飞跃,将主要依赖于计算机技术的发展和不同学科背景科学家的技术碰撞。一方面,计算机技术的发展使人类能够解决复杂且难以处理的问题。另一方面,计算机技术能够有效激发有序复杂性问题的新解决方法。这种新解决方法本身也正是计算科学(computational science)的范畴之一,让科学家有机会集中资源,将不同领域的见解聚焦在共同问题上。这种见解聚焦的结果,促使不同学科背景的科学家们,形成比单一学科背景科学家们更强大的“混合团队”;这样的“混合团队”将有能力解决某些复杂性问题,并且得出有用的结论。总之,科学和建模紧密相关,模拟执行代表理论的模型,人们把科学研究中的计算机模拟称为科学模拟(scientific simulation)。
目前,还没有任何针对“计算机模拟”的单一定义能够恰当地描述科学模拟的概念。美国国防部将模拟定义为一种方法,即:“一种随时间实现模型的方法”;进而,将计算机模拟定义为一种过程,即:“在计算机上执行代码、控制和显示接口硬件,并与现实世界设备进行接口交互的过程”。Winsberg把计算机模拟的定义又分为狭义和广义范围。
在狭义定义中,计算机模拟就是“在计算机上运行程序的过程”。计算机模拟使用步进方法来探索数学模型的近似行为。模拟程序在计算机上的一次运行过程,代表了对目标系统的一次模拟。人们愿意用计算机模拟方法求解问题,主要有以下2个原因:原始模型本身包含离散方程;原始模型的演化更适合用“规则”,而不是“方程”来进行描述。值得注意的是,这种狭义角度指代计算机模拟时,需要限定到特定处理器硬件上算法的实现、用特定编程语言编写应用,以及核函数程序、使用特定编译器等限制条件。在不同应用问题的场景下,由于这些限制条件的变化,通常会获得不同的性能结果。
在广义定义中,可以把计算机模拟看作研究系统的一种综合方法,是更加完整的计算过程。该过程包括模型选择、通过模型实现、算法输出计算、结果数据可视化及研究。整个模拟的过程也可以与科学研究过程进行对应,如Lynch所描述:提出一个经验上可回答的问题;从旨在回答该问题的理论中推导出一个可证伪的假设;收集(或发现)和分析经验数据以检验该假设;拒绝或未能拒绝该假设;将分析结果与得出该问题的理论联系起来。在过去,这种广义的计算机模拟通常出现在认识论或者方法论的理论场景中。
Winsberg进一步将计算机模拟划分为基于方程的模拟(equation-based simulation)和基于主体的模拟(agent-based simulation)。基于方程的模拟常用于物理等理论学科中。这些学科中一般存在主导性的理论,这些理论可以用来指导构建基于微分方程的数学模型。例如,基于方程的模拟可以是针对粒子的模拟,这种模拟通常包含数量巨大的多个独立粒子和一组描述粒子之间相互作用的微分方程。此外,基于方程的模拟也可以是基于场的模拟,通常包含一组描述连续介质或场的时间演化方程。基于主体的模拟往往遵循某种演化规则,是模拟社会和行为科学的最常见方式。例如, Schelling的隔离政策模型。尽管基于主体的模拟在一定程度上可以表示多个主体的行为,但与基于方程的粒子模拟不同,这里没有控制粒子运动的全局微分方程。
从计算机模拟的定义和分类中,可以看出人们对科学模拟不同层次的期望。从狭义的计算机模拟角度看,它已包養網经成为理论分析和实验观察等传统认知方式的补充手段。科学或工程领域无一例外是由计算机模拟推动的,在某些特定应用领域和场景下,甚至是由计算机模拟改变的。如果没有计算机模拟,许多关键技术就无法被理解、开发和利用。广义的计算机模拟蕴含着一个哲学问题:计算机是否可以自主进行科学研究?科学研究的目标是认识世界,这意味着计算机程序必须创造新的知识。随着人工智能技术研究及应用的新一轮爆发,人们对计算机自动地以“智能”方式进行科学研究充满了期待。值得一提的是,Kitano在2021年提出的“诺贝尔-图灵挑战”的新观点——“到2050年,开发能够自主执行研究任务的智能科学家,做出诺贝尔奖级别的重大科学发现”。该观点涉及狭义和广义的计算机模拟相关技术,但没有围绕广义定义的“哲学问题”深入探讨,只是把其作为科学模拟的一个宏伟目标看待。
科学模拟的发展阶段
从最直观的视角来看,科学模拟的载体是计算机程序。从数学形式上讲,计算机程序是由可计算函数组成的,其中每个函数将有限输入数据的离散集映射到有限输出数据的离散集上。从计算机技术上讲,计算机程序等于算法加上数据结构。因此,科学模拟的实现需要以科学问题及其解决方式被形式化抽象为条件。这里,本文借用Simon的观点:科学家即问题“求解器”。在此观点中,科学家给自己设定了重大科学问题,确定问题和解决问题的策略和技术是科学发现的本质。基于上述“求解器”的话语体系,本文类比求解方程的形式,将科学模拟的发展划分为3个阶段,即数值计算、模拟智能和科学大脑(图1)。
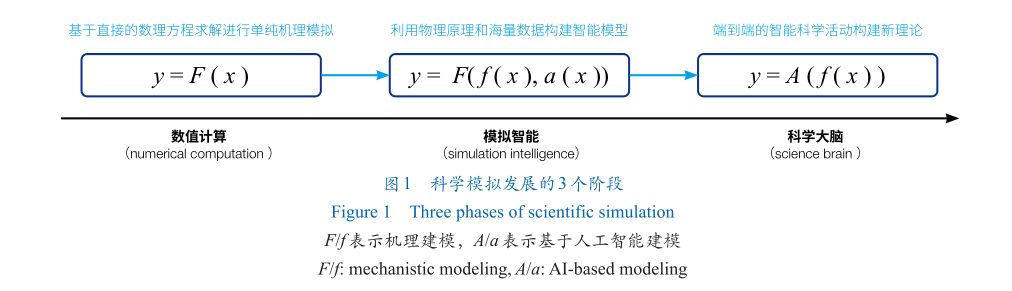
数值计算
然而,这种将部分复杂科学问题转换为相对简单的计算问题的解题模式,仅仅是一种粗粒度的建模方案,在一些应用场景下会遇到计算瓶颈。在解决真实场景中复杂物理模型时,常常面临基本物理原理计算量过大的问题,并由此导致空有原理而无法有效解决科学问题。例如,第一性原理分子动力学的关键为求解量子力学Kohn-Sham方程,其核心算法求解过程是多次求解大规模特征值问题。特征值问题的计算复杂度为N3(N为矩阵的维度)。在实际物理问题的求解中,最常用的平面波基组通常是原子个数的100—10000倍。这意味着对于上千原子的体系规模,矩阵维度N达到106,其相应的浮点数运算总量也将达到1018 FLOPS,即达到EFLOPS级别的计算量。需要注意的是,在单步分子动力学中需要多次求解特征值问题,这也就使得单步分子动力学的模拟时间通常为数分钟乃至1小时。由于单步分子动力学的模拟物理时间只能达到1飞秒,假设要完成纳秒物理时包養網间的分子动力学模拟过程,就需要106个分子动力学步。相应的计算量至少要达到1024 FLOPS。如此庞大的运算量即使使用世界上最大规模的超级计算机也难以在短时间内完成。为了解决仅使用第一性原理计算带来的超大计算量,研究人员发展了多尺度方法,其中最典型的是获得了2013年诺贝尔化学奖的量子力学/分子力学(QM/MM)方法。该方法的思想是针对核心物理化学反应部分(如:酶及其结合底物的活跃位点原子),采用高精度的第一性原理计算方法,对于周围的物理化学反应区域(溶液、蛋白质和其他区域)采用低精度且计算复杂度更低的经典力学方法。这种高精度、低精度相结合的计算方法,可以有效地降低计算量。但面对实际问题时,该方法依然存在着巨大的挑战。例如,细胞半径约0.2微米的单个生殖支原体包含3×109个原子和77000个蛋白质分子。由于核心计算时间仍来自QM部分,模拟2小时的过程预计需要耗费109年。如果将类似问题推广到人脑的模拟中,相应的系统原子数将达到1026个,保守估计需要1010个活跃位点的QM计算。由此可以推断,模拟1小时的QM部分需要长达1024年的时间,而MM部分的模拟也需要长达1023年的时间。这种超长计算时间的情况也被称为“维度灾难”。
模拟智能
因此,模拟智能在传统数值计算中嵌入人工智能模型(当前主要是深度学习模型),不同于其他人工智能应用领域的深度学习模型“黑盒子”。模拟智能要求这些模型的基本出发点和基本结构是可解释的。目前,这一方向已存在大量研究,Zhang等在2023年对模拟智能领域最新进展进行了系统性的梳理。从理解亚原子(波函数和电子密度)、原子(分子、蛋白质、材料和相互作用)到宏观(流体、气候和地下)尺度物理世界,把研究对象分为量子(quantum)、原子(atomistic)和连续介质(continuum)三大体系,涵盖量子力学、密度泛函、小分子、蛋白质、材料科学、分子间相互作用和连续力学等7个科学领域。此外,还详细讨论了其中关键的共同挑战,即:如何通过深度学习方法捕捉物理第一性原理,特别是自然系统中的对称性。利用物理原理的智能模型几乎已经渗透了传统科学计算的所有领域。模拟智能大幅提升了对微观多尺度系统的模拟能力,为在线实验反馈迭代提供了更加全面的支撑条件。例如,计算模拟系统和机器人科学家之间的快速实时迭代,有助于提升科研效率。因此,模拟智能在一定程度上,还将包括“理论—实验包養網”迭代的控制过程,同时也会涉及部分广义的科学模拟。
科学大脑
传统的科学方法从根本上塑造了人类探索自然和科学发现的分步“指南”。面对全新的研究问题,科学家们已经被训练成从假设和替代方案的角度出发,指定如何开展控制测试的定势思维。虽然这种研究过程在过去几个世纪内都是有效的,但是非常缓慢的。从某种意义上来说,这种研究过程是主观的,是由科学家的聪明才智和偏见驱动的。这种偏见,有时会阻碍必要的范式转变。人工智能技术的发展激发了人们对科学和智能融合产生最优的且具有创新性的解决方案的期望。
以上所提到的科学模拟发展经历的3个阶段,能够明显区分计算机模拟在可计算和智能化能力方面逐步提升的过程。数值计算阶段,对复杂科学问题中相对简单的计算问题进行了粗粒度建模,属于单纯的狭义计算机模拟定义范畴。它不仅促进众多领域宏观尺度科学发现,同时也开启了对微观世界的初步探索。模拟智能阶段,将针对微观世界的多尺度探索推上一个新的台阶。除了在狭义计算机模拟定义范畴内对计算能力进行了数量级地提升之外,该阶段还涉及对实验中某些关键环节的计算加速,在一定程度上为科学模拟下一阶段的实现奠定了基础。科学大脑阶段,将是对广义计算机模拟定义的实现。在此阶段中,计算机模拟将具备创造知识的能力。
设计模拟智能计算系统的关键问题
按照本文对科学模拟发展阶段的粗粒度划分,与其相应的计算系统也在同步进化。超级计算机在数值计算阶段发挥了不可替代的作用;发展到新的模拟智能阶段,底层计算系统的设计也是基石。那么,模拟智能计算系统的发展方向应该遵循什么样的指导思想?
纵观计算和科学研究发展历史,可归纳出计算系统发展的基本周期性规律:在新的计算模式和需求产生阶段的初期,计算系统的设计侧重追求极致的专用性。而在经过一段时间的技术演变和应用拓展之后,计算系统的设计开始侧重于对通用性的追求。在人类科技文明早期发展的漫长过程中,计算系统曾经是各式各样的专用机械设备,辅助进行一些简单的运算(图2)。近代以来,电子技术的突破催生了电子计算机的出现,并且随着其计算能力的不断提升,数学、物理等学科的发展也不断向前,尤其是超级计算机上的大规模数值模拟成果,引领了大量前沿科学研究和重大工程应用。由此可见,日益发展的通用高性能计算机在不断地加速宏观尺度科学的各类大规模应用,并取得重大成果。接下来,微观世界的多尺度探索将是未来Z级(1021)超级计算机应用的核心场景。而现有通用高性能计算机的技术路线则将遇到功耗和效率等瓶颈,难以为继。结合模拟智能阶段所呈现的新特征,本文认为面向模拟智能的计算系统,将以追求极致的Z级计算专用智能系统为设计目标,未来性能最高的计算系统将专门针对模拟智能应用程序,在硬件本身及软件底层的算法和抽象中进行定制。
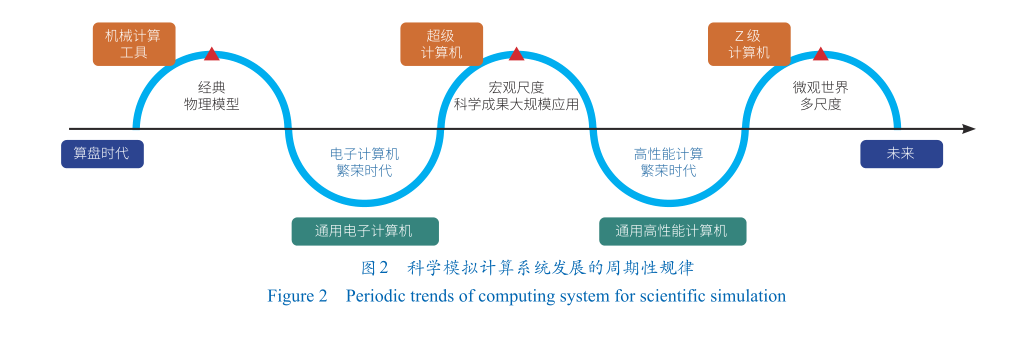
图2 科学模拟计算系统发展的周期性规律
Figure 2 Periodic trends of computing system for scientific simulation
直观上讲,面向模拟智能的计算系统离不开智能组件(软件和硬件),那么基于现有的智能组件来构建智能计算系统就能真正满足模拟智能的需求吗?答案是否定的。李国杰院士曾经指出:“有人曾戏谑目前信息领域的形势为:‘软件在吞噬世界,人工智能在吞噬软件,深度学习在吞噬人工智能,GPU(图形处理器)在吞噬深度学习。’”研究制造更高性能的GPU或类似的硬件加速器,似乎成了对付大数据的主要出路。但是如果不清楚该在什么地方加速,只盲目依靠硬件的蛮力是不明智的。因此,设计智能系统的关键在于深刻理解要求解的问题。计算机架构师的角色是选择好的知识表示、识别开销密集型任务、学习元知识、确定基本操作后,再用软硬件优化技术去支持这些任务。”
面向模拟智能的计算系统设计是一个新产生的研究主题,相对其他计算系统设计而言,更加具有显著的独特性。因此,需要一个整体统一的视角,来推进人工智能和模拟科学的交叉。1989年,Wah和Li总结了关于智能计算机系统设计的3个层次,该观点至今依然值得借鉴。但遗憾的是,目前还没有任何关于这方面的更加深入的讨论和实际性研究。具体而言,智能计算机系统的设计要考虑3个层次——表示层(representation level)、控制层(control level)和处理层(processor level)。表示层处理用于解决给定人工智能问题的知识和方法,以及如何表示该问题;控制层关注算法中依赖关系和并行性,以及问题的程序表示;处理层解决执行算法和程序表示所需的硬件和体系结构组件。下面将以这3个层次为基础,讨论面向模拟智能的计算系统设计的关键问题。
表示层
表示层是设计过程中的一个重要元素,包括领域知识表示和共性特征(元知识)表示,其决定了给定问题是否能够在合理的时间内得到解决。定义表示层的本质是对适应广泛应用的行为和方法进行高级抽象,将它们与特定的实现解耦。下面给出领域知识表示和共性特征表示的案例。
从现阶段面向科学的人工智能研究看,对称性的研究将成为表征学习的一个重要突破口,其原因在于物理上的守恒定律是由对称性导致的(诺特定理),而守恒定律常被用来研究粒子的基本属性和粒子之间的相互作用。物理上的对称性是指在某种变换后或某种操作下的不变性,无法做出可辨别的测量(不可区分性)。基于多层感知机(MLP)、卷积神经网络(CNN)、图神经网络(GNN)的小分子表征模型在有效加入对称性之后,已经广泛应用于蛋白质、分子、晶体等物质的结构预测。
2004年,Colella向美国国防高级研究计划局(DARPA)提出了科学计算的“七个小矮人”(Seven Dwarfs)——稠密线性代数、稀疏线性代数、结构网格计算、非结构网格计算、谱方法、粒子方法、蒙特卡洛模拟。其中,每一种科学计算问题,都代表了一种可以捕获计算和数据移动模式的计算方法。受此启发,巴斯德实验室的Lavin等以类似方式定义了模拟智能中的9种基元(nine motifs of simulation intelligence)——多物理现象多尺度建模、代理建模仿真、基于模拟的推理、因果关系建模推理、基于主体的建模、概率编程、微分编程、开放式优化、机器编程。这9种基元代表了互为补充的不同计算方法类型,为协同模拟和人工智能技术促进科学发展奠定了基础。面向传统科学计算归纳的各个主题,曾为应用于不同学科的数值方法(以及并行计算)的研发工作提供了明确的路线图;面向模拟智能的各个主题同样不局限于狭义的性能或程序代码,而是激励算法、编程语言、数据结构和硬件方面的创新。
控制层
控制层承上启下,在整个计算系统中起到连接和控制算法映射与硬件执行的关键作用,在现代计算机系统中表现为系统软件栈。本文仅讨论和科学模拟相关的关键组件。模拟智能计算系统的控制层的变化主要来自2个方面:数值计算、大数据和人工智能的紧耦合;底层硬件技术可能发生的颠覆性变化。近年来,由于科学大数据的急剧增加,在科学模拟的数值计算阶段,大数据软件栈逐渐被超算系统领域所关注,只是相对于传统的数值计算,大数据软件栈是完全独立的,在模拟流程上属于不同的步骤。因此,基于2套系统的软件栈是基本可行的。而在模拟智能阶段,情况产生了根本上的变化。根据前文中所表示的问题解法描述公式y=F(f(x),A(x)),人工智能和大数据部分都是嵌入在数值计算内的,这种包養網结合是一个紧耦合的模拟过程,自然需要一个异质融合的系统软件栈。以DeePMD为例,该模型包含平移不变性的嵌入网络、对称性保持操作和拟合网络3个模块。鉴于体系的能量、受力等属性不以人为定义改变(例如,便于测量或描述而赋予体系中各个原子的坐标),接入拟合网络进行原子能量和受力的拟合,就能得到较高精度的拟合结果。再考虑模型的训练数据强依赖于第一性原理计算,整个流程是一个数值计算和深度学习紧耦合的过程。
因此,系统软件在代码生成和运行时执行过程中,将不再区分共性核函数的来源,即不再区分是否由传统人工智能、传统数值计算或根据特定问题进行人工定制扩展得来。相应的,系统软件一方面需要针对3类不同来源的共性核函数,提供易于扩展和开发的编程接口。另一方面则需要对这3类函数,在代码编译方面和运行时资源管理方面,兼顾并行效率和访存局部性等性能保障;在面向不同粒度的计算任务时,能够逐层进行融合和协同优化,发挥不同类型体系结构处理器的最佳性能。
处理层
纵观数值计算阶段到模拟智能阶段,一个驱动技术发展的重要因素是当前硬件技术无法满足计算需求。因此,处理层设计首要问题是:表示层的变化(如对称性、基元)会产生全新的硬件体系架构吗?它们是基于传统专用集成电路(ASIC)实现,还是超越互补金属氧化物半导体(CMOS)——从高性能计算的发展路线图来看,这也是未来Z级超算的硬件设计要考虑的核心问题。可以大胆预测,在2035年左右,Z级超算可能会出现。尽管基于性能和可靠性因素的考虑,那时CMOS平台仍将占据主流,但一些核心组件将是建立在非CMOS工艺上的专用硬件。
摩尔定律虽然放缓但依然有效,要重点解决的关键难题是如何逼近摩尔定律的极限。换句话说,如何通过软硬件协同设计的手段,将基于CMOS的硬件潜力充分挖掘出来。因为,即使在性能优先级最高的超算领域,多数算法负载所获得的实际性能仅仅只是硬件裸性能的极小部分。回顾超算领域早期发展阶段,其基本设计哲学就是软硬件协同。未来十几年,微处理器迅速发展的“红利”将耗尽,面向模拟智能的计算系统硬件架构应该回归到从头设计的软硬件协同技术上。一个突出的例子是如前所述的分子动力学模拟,Anton系列是一个从零开始设计的超级计算机家族,可以满足大规模长时间尺度的分子动力学模拟计算,而这也恰恰是对微观世界探索的必要条件之一。然而,最新的Anton计算也只能对基于经典力场模型实现20微秒的模拟,无法进行第一性原理精度的长时间尺度模拟;然而,后者才能满足多数实际应用(如药物设计等)需求。
最近,作为模拟智能的典型应用,DeePMD模型在传统大规模并行系统上的突破证明了其巨大的潜力。中国科学院计算技术研究所超算团队,已实现了170个原子的第一性原理精度分子动力学的纳秒级模拟。但是,长时间尺度模拟要求硬件架构具有极高的可扩展性,需要在运算逻辑和通信操作上有极致的创新。本文认为有2类技术可以预期能够发挥关键作用:存算一体架构,通过降低数据移动的延迟来提高运算效率;硅光互连技术,可以在高能效下提供大带宽的通信能力,有助于提高并行性和数据规模。进而,随着对模拟智能应包養網用广泛而深入的研究,相信未来将逐步形成科学模拟领域的“新浮点”运算单元和指令集。
本文认为,在科学模拟的现阶段,尚处于模拟智能阶段的早期,此时对模拟智能的使能技术展开研究至关重要。在一般科学研究中,独立的概念、关系和行为可能是易理解的。但是,它们的组合行为会导致不可预测的结果。深入了解复杂系统的动态行为,对于许多处理复杂挑战性领域的研究人员来说是非常宝贵的。在面向模拟智能的计算系统设计中,一个必不可少的环节是跨学科合作,即领域科学、数学、计算机科学与工程、建模与仿真等学科工作者之间的协作。这种跨学科合作会构建更优的模拟计算系统,形成更全面和整体的方法,去解决更加复杂的现实世界的科学挑战。
(作者:谭光明、贾伟乐、王展、元国军、邵恩、孙凝晖,中国科学院计算技术研究所。《中国科学院院刊》供稿)
發佈留言